Prof. Dr. Julio RODRIGUEZ

Prof. Dr. Julio RODRIGUEZ |

|
Left, under SYNCHRONIZATION, you see seven oscillators, initially uncoupled (i.e. no black lines showing the network's interactions), each with its own frequency. When the network's interactions are introduced (i.e. black lines appearing in the animation), all oscillators synchronize (converge to a common frequency). However, as soon as the network interactions are removed, all oscillators go back to their own frequency. On the left, under ADAPTATION, you see the same set up, but here the oscillators are equipped with an adaptive frequency mechanism. Once they interact through the network, not only do they fully synchronise (to a common frequency and the same phase), they adapt to one another: when the network's interactions are removed, all oscillators continue to oscillate with the consensual frequency.
|
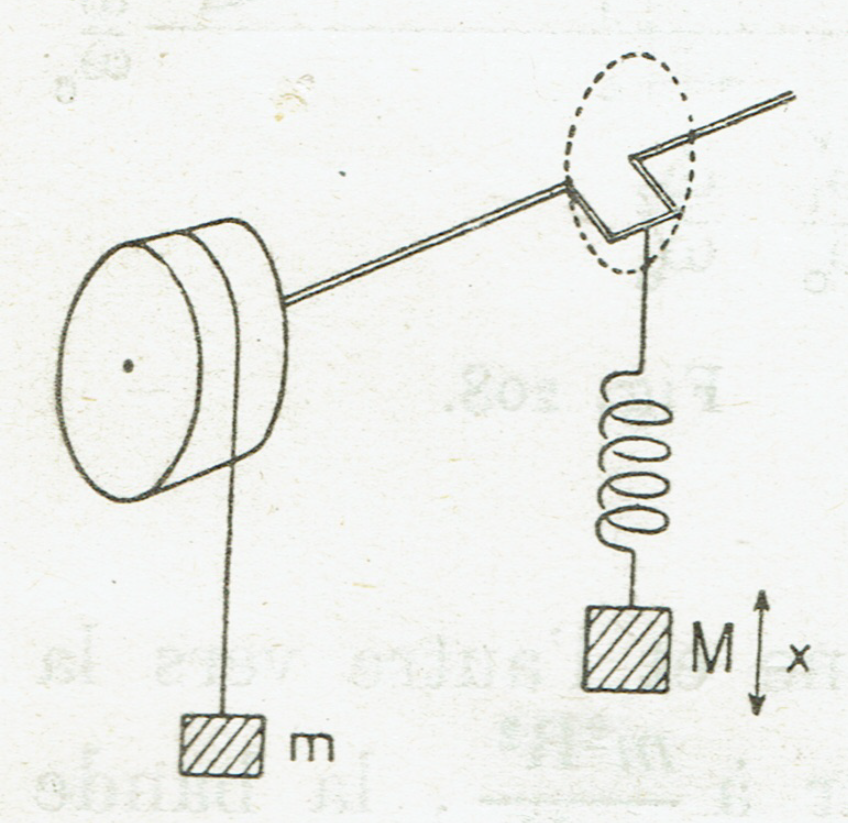
$$
\Large{
\begin{array}{rcl}
(\mathsf{I} + m\rho^{2}) \ddot{\theta} + h \dot{\theta} & = & mg \rho + \mathsf{K} ( x - a \sin(\theta) ) a\cos(\theta) \\
& & \\
\mathsf{M} \ddot{x} + f \dot{x} & = & \mathsf{M}g - \mathsf{K} ( x - a \sin(\theta) )
\end{array}
}
$$
9 control parameters: - drum: radius \( \rho \), inertial moment \( \mathsf{I} \), suspended mass \( m \), friction \( h \) - spring: stiffness coefficient \( \mathsf{K} \), suspended mass \( \mathsf{M} \), gravitation acceleration \( g \), friction \( f \) - rotating spit: crank/handel radius \( a \) |
|